Shridharacharya: Solving Quadratic equations in the 9th Century.

on

Sridhar Acharya (c. 870, India – c. 930 India) was an Indian mathematician, Sanskrit pundit andphilosopher. He was born in Bhurishresti (Bhurisristi or Bhurshut) village in South Radha (at present Hughli) in the 10th Century AD.

He was known for two treatises: Trisatika(sometimes called the Patiganitasara) and thePatiganita. His major work Patiganitasara was named Trisatika because it was written in three hundred slokas. The book discusses counting of numbers, measures, natural number, multiplication, division, zero, squares, cubes, fraction, rule of three, interest-calculation, joint business or partnership and mensuration.

He was one of the first to give a formula for solving quadratic equations.He found the formula :-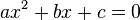

 (Multiply by 4a)

Proof of the Sridhar Acharya Formula,

let us consider,

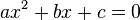
ax^2 + bx + c = 0

  • Multipling both sides by 4a,

4a^2x^2 + 4abx + 4ac = 0

  • Substracting 4ac from both sides,

4a^2x^2 + 4abx = -4ac

  • Then adding b^2 to both sides,

4a^2x^2 + 4abx + b^2= - 4ac + b^2

  • We know that,

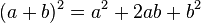
(a + b)^2 = a^2 + 2ab + b^2

  • Using it in the equation,

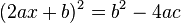
(2ax + b)^2 = b^2 - 4ac

  • Taking square roots,

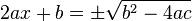
2ax + b = \pm\sqrt{b^2 - 4ac}

2ax = -b\pm\sqrt{b^2 - 4ac}

  • Hence, dividing by 2a get

x=\frac{-b\pm\sqrt{b^2-4ac\ }}{2a}.

In this way, he found the proof of 2 roots.(http://en.m.wikipedia.org/wiki/Sridhara)

Comments

Post a Comment